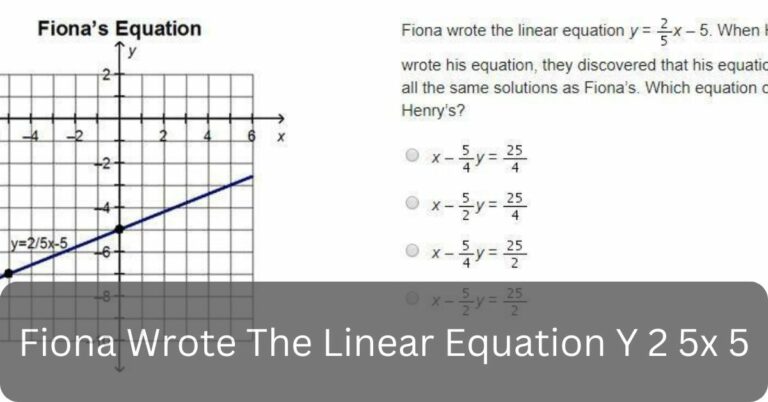
When I found math hard, Fiona Wrote The Linear Equation Y 2 5x 5 made me think. Like Fiona, I had to try hard to understand linear equations.
Fiona Wrote The Linear Equation Y 2 5x 5 showing her learning about math. This equation signifies Fiona’s journey in understanding linear relationships, highlighting the importance of math education and personal growth.
We’ll explore what this equation means and how it relates to Fiona’s learning experience with math. Let’s uncover the story behind Fiona’s mathematical journey together.
What Is The Linear Equation Y 2 5x 5 – The World Of Math!

The linear equation y = 2 + 5x + 5 represents a relationship between two variables, x and y, in a straight line form. In this equation:
- y represents the dependent variable,
- x represents the independent variable,
- 2 and 5 are constants, and
- 5x represents the term where x is multiplied by 5.
Understanding this equation allows us to analyze how changes in x affect y and vice versa, which is essential in various mathematical and real-world applications.
How To Understand The Linear Equation Y 2 5x 5 – Let’s Take A Look!
Understanding the linear equation y = 2 + 5x + 5 involves several steps:
- Identify Variables: In this equation, y and x are variables. y represents the dependent variable, and x represents the independent variable.
- Examine Terms: Break down the equation into individual terms. Here, we have 2, 5x, and 5.
- Understand Relationships: Recognize how the terms are related. 5x indicates that x is multiplied by 5, and 2 and 5 are constants.
- Interpret Constants: Constants like 2 and 5 are fixed values that do not change. They represent specific points on the graph.
- Visualize Graphically: Plot the equation on a graph to see how it forms a straight line. The slope of the line is 5, and the y-intercept is 2 + 5 = 7.
Understanding linear equations helps analyze relationships between variables and make predictions based on the given information.
Who Is Fiona – Join Her Mathematical Journey!
Fiona is a hypothetical person mentioned in the context of a mathematical scenario. She represents an individual who has written or is associated with a specific equation or problem.
In this case, she is referenced alongside a linear equation, suggesting her involvement in mathematical exploration or learning.
Why The Linear Equation Y 2 5x 5 Important – Explore Its Impact!
- Modeling Relationships: It helps us model and understand relationships between variables straightforwardly.
- Predictions and Analysis: With this equation, we can make predictions and analyze how changes in one variable affect the other, which is crucial in fields like economics, physics, and engineering.
- Problem Solving: It equips us with problem-solving skills, allowing us to tackle real-world problems by translating them into mathematical equations and finding solutions.
- Foundation for Further Learning: Linear equations are the foundation for more complex mathematical concepts, making it essential to grasp them thoroughly for further learning in mathematics and related disciplines.
Can You Tell Me What Each Part Of “Fiona Wrote The Linear Equation Y 2 5x 5 ” Means?

- “y” represents the output or dependent variable. It’s the value we’re trying to find or predict.
- “2” is a constant term, meaning it’s a fixed number and doesn’t change. It’s called the y-intercept, indicating where the line crosses the y-axis.
- “5x” is a term where “x” is multiplied by 5. It represents the slope of the line, indicating how much y changes for every unit increase in x.
- “5” is another constant term, similar to the first one. It’s also part of the y-intercept and helps determine the position of the line on the graph.
Why Is “Fiona Wrote The Linear Equation Y 2 5x 5” Called A Straight Line Equation?
Fiona Wrote The Linear Equation Y 2 5x 5″ is called a straight line equation because when graphed, it represents a straight line.
In this equation, the variable “y” depends linearly on the variable “x,” meaning that for each increase in “x,” there’s a consistent change in “y.” This linear relationship between “x” and “y” results in a straight line when plotted on a graph.
How Would You Draw The Picture For “Fiona Wrote The Linear Equation Y 2 5x 5 “?
To draw the graph of the equation y = 2 + 5x + 5, follow these steps:
- Plot the y-intercept: Start at the point 0, 2 + 5, which is 0, 7 on the coordinate plane.
- Find another point using the slope: Since the coefficient of x is 5, the slope is 5. This means for every increase of 1 in x, y increases by 5.
So from the y-intercept, move 1 unit to the right and 5 units up to plot another point. Draw a straight line through these two points to represent the equation on the graph.
Repeat these steps to plot more points and ensure the line is straight. This line represents all the solutions to the equation y = 2 + 5x + 5.
What Happens If We Change The Numbers In “Fiona Wrote The Linear Equation Y 2 5x 5 “?

If we change the numbers in the equation “Fiona Wrote The Linear Equation Y 2 5x 5,” it will alter the properties of the line represented by the equation:
1. Y-Intercept (Constant Term): Changing the constant term (2 or 5) will shift the line-up or down along the y-axis. A positive change will move it up, while a negative change will move it down.
2. Slope (Coefficient of x): Altering the coefficient of x (5 in this case) will change the steepness or slope of the line. A more significant coefficient will make the line steeper, while a smaller coefficient will make it less steep.
3. Overall Position and Angle: Adjusting both the y-intercept and the slope will change the overall position and angle of the line on the graph.
Changing the numbers in the equation modifies the characteristics of the line, but it will still represent a linear relationship between x and y.
Frequently Asked Questions:
1. How does Fiona Wrote The Linear Equation Y 2 5x 5 relate to real-world problems?
Fiona’s equation represents a linear relationship between two variables and can be used to model various scenarios such as distance-time relationships, cost analysis, or revenue prediction in business.
2. Can Fiona Wrote The Linear Equation Y 2 5x 5 be expressed differently?
Fiona’s equation can be rearranged into slope-intercept form, y = mx + b, where m represents the slope and b represents the y-intercept. For example, y = 5x + 7.
3. What mathematical concepts can be explored by studying Fiona Wrote The Linear Equation Y 2 5x 5 ?
Studying Fiona’s equation involves understanding constants, variables, slopes, y-intercepts, and fundamental concepts in algebra and graphing linear equations.
4. How can understanding Fiona Wrote The Linear Equation Y 2 5x 5 , help improve problem-solving skills?
Understanding Fiona’s equation enhances problem-solving skills by enabling individuals to analyze relationships between variables, make predictions, and solve real-world problems efficiently.
Conclusion:
Fiona Wrote The Linear Equation Y 2 5x 5 which helps us understand basic math relationships. Studying this equation teaches us about constants, variables, and how numbers work together. Her equation is valuable for solving problems and understanding how math applies to real life.